Joint Probability

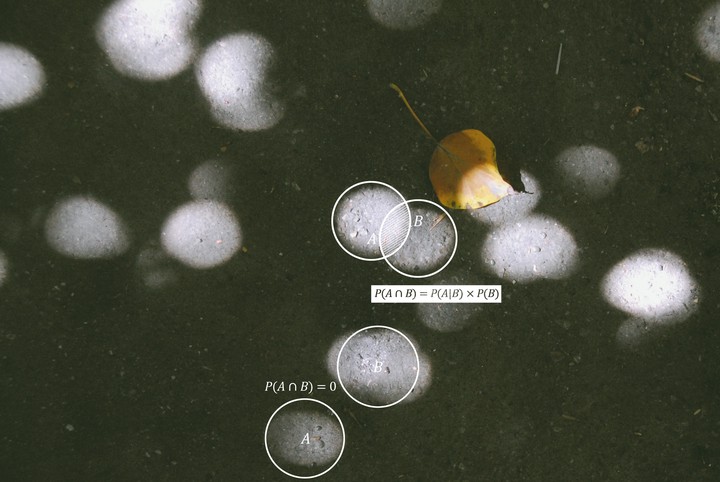
A and B are two separate events, but not necessarily completely separate. Sometimes A and B can happen together. The probability of that occurring is given by \(P(A \cap B)\): the joint probability. \(P(A \cap B)\) can be a pain to calculate; it’s easiest to deduce visually, but that isn’t always possible. However, in the special case in which A and B are known to be mutually exclusive (that is, they never occur together), you know that the joint probability is automatically zero: knowing something about A says nothing about B.

One roundabout way of finding the joint probability is by multiplying the probability of B occurring by the probability A occurring when you already know that B has occurred (the conditional probability). Not very direct, but really informative about the world. It’s hard to predict the probability of just one event occurring, but if you know that its “joint” event already occurred, you know so much more.